目标

项目中为了减少打包后的包体大小，针对 IL2CPP 的打包方案做包体缩小的优化

问题

IL2CPP 虽然在性能上比 mono 有优势，但是当代码量增多时，包体会增大

研究

2015 年的一篇帖子有提到 IL2CPP 在打包时会将未使用的属性打包进 IL 中，作者测评下来发现修改裁剪工具，剔除不需要的属性能减少 6% 的 IL2Cpp 大小。
原帖地址
在 unity2017 版本中，并没有作者所提到的 UnusedByteCodeStripper2.exe 工具，推测 unity 可能在后续版本更新中做了优化。

测试 Attribute 的优化

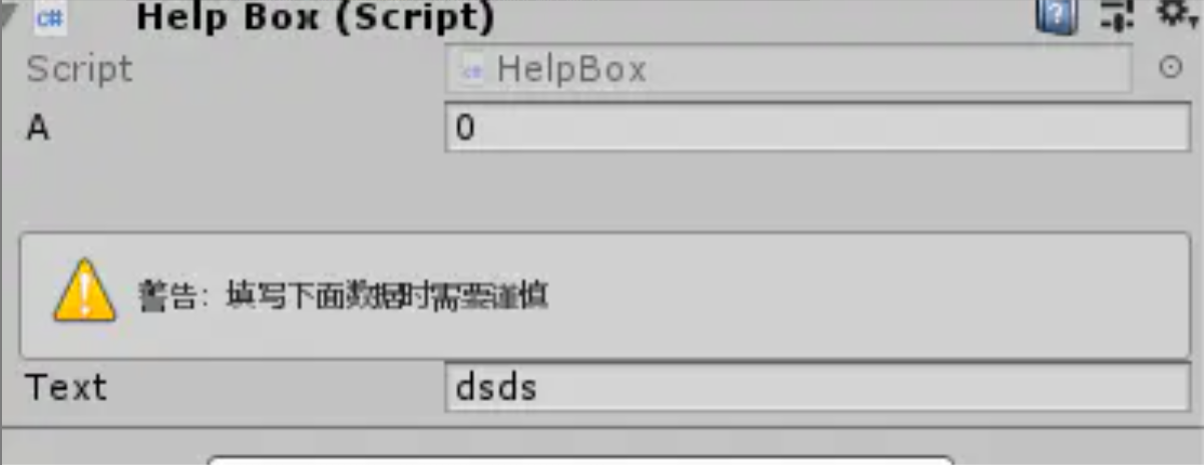
新建空的项目工程，创建 test.cs , 对其中的 test 字段使用属性元数据。 选择 IL2Cpp 打包方案打包 apk 包，使用 IL2Cppdumper ，反编译查看包体中的 libil2cpp.so ， 对比查看使用了属性以及未使用属性的打包结果。

目标

项目中为了减少打包后的包体大小，针对 IL2CPP 的打包方案做包体缩小的优化

问题

IL2CPP 虽然在性能上比 mono 有优势，但是当代码量增多时，包体会增大

研究

2015 年的一篇帖子有提到 IL2CPP 在打包时会将未使用的属性打包进 IL 中，作者测评下来发现修改裁剪工具，剔除不需要的属性能减少 6% 的 IL2Cpp 大小。
原帖地址
在 unity2017 版本中，并没有作者所提到的 UnusedByteCodeStripper2.exe 工具，推测 unity 可能在后续版本更新中做了优化。

测试 Attribute 的优化

新建空的项目工程，创建 test.cs , 对其中的 test 字段使用属性元数据。 选择 IL2Cpp 打包方案打包 apk 包，使用 IL2Cppdumper ，反编译查看包体中的 libil2cpp.so ， 对比查看使用了属性以及未使用属性的打包结果。

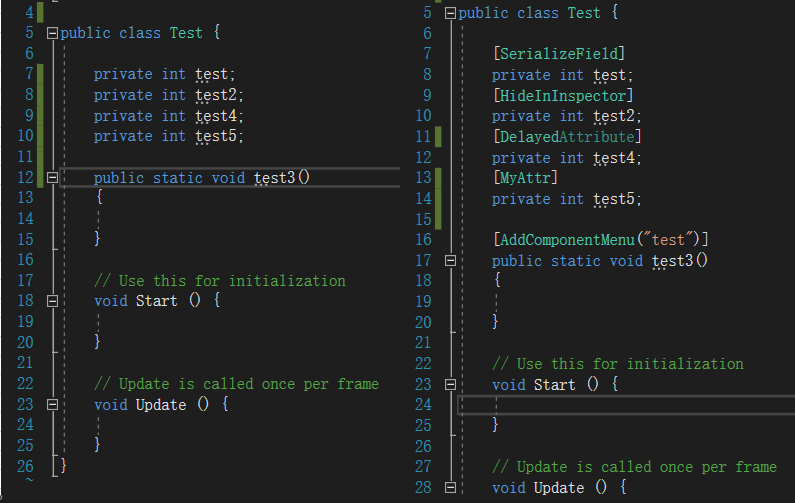
未使用属性的 attribute 在反编译结果中未找到对应的声明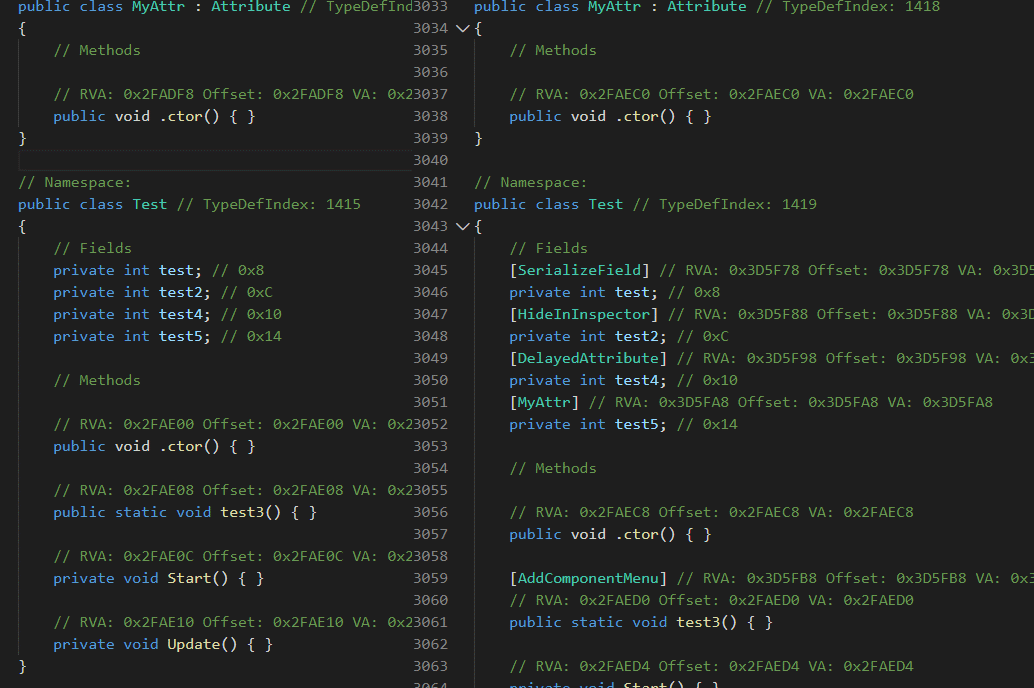

Managed bytecode stripping with IL2CPP

查找文档发现 unity2017 已经新增了对 IL 代码的裁剪选项，此选项开启后会使用 UnityLinker(is a version of the Mono IL Linker) 对引擎中未引用的代码进行剔除。
剔除工作是基于代码的静态分析，需要注意以下情况，并处理。

• 如果代码中使用了反射来引用，可能会出现运行时引用类型被剔除的报错。
• 项目打包中会有 prefab 资源的提前构建 ab 包，此构建过程在 UnityLinker 调用之前执行，一些类型的引用只存在与 Prefab 中，也会出现类型丢失问题。需要手动排查并引用进 mono 防止类型被剔除。

执行

对裁剪后的包进行冒烟测试，查找并修复类型丢失的问题。

运行时，unity 会抛出类型丢失的错误，并附带一个应用 ID， 通过 ClassIDRefrence 查找，获知对应的类型。

反射引用

测试下来并未出现有相关类型报错的问题，说明代码中没有通过这种方法对类型进行引用。

资源 ab 包

出现一些 Prefab 引用类型丢失的情况，新增 link.xml 放置在 Assets 下，指导 UnityLinker 的剔除保留。

1
2
3
4
5
6
7
8
9
10
11
12
13

<?xml version="1.0" encoding="utf-8" ?>
<linker>
    <assembly fullname="System">
        <type fullname="System.ComponentModel.TypeConverter" preserve="all" />
    </assembly>
    <assembly fullname="mscorlib">
        <namespace fullname="System.Security.Cryptography" preserve="all"/>
    </assembly>
    <assembly fullname="UnityEngine">
        <type fullname="UnityEngine.Flare" preserve="all"/>
        <type fullname="UnityEngine.Avatar" preserve="all"/>
    </assembly>
</linker>

结果

最终包体缩小 34MB

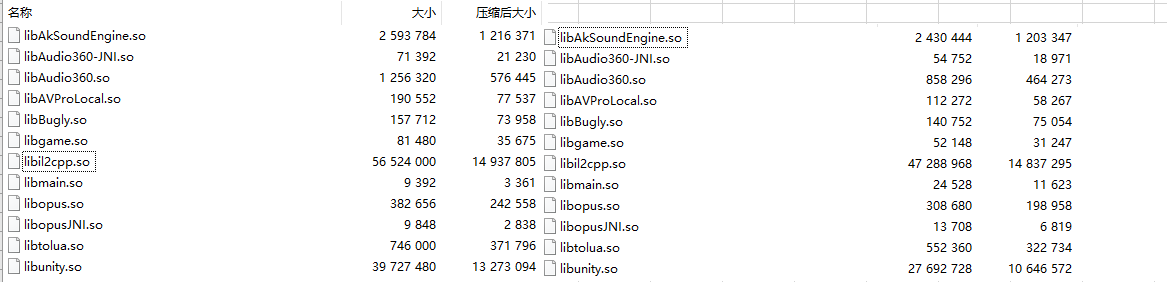
未使用属性的 attribute 在反编译结果中未找到对应的声明

目标

项目中为了减少打包后的包体大小，针对 IL2CPP 的打包方案做包体缩小的优化

问题

IL2CPP 虽然在性能上比 mono 有优势，但是当代码量增多时，包体会增大

研究

2015 年的一篇帖子有提到 IL2CPP 在打包时会将未使用的属性打包进 IL 中，作者测评下来发现修改裁剪工具，剔除不需要的属性能减少 6% 的 IL2Cpp 大小。
原帖地址
在 unity2017 版本中，并没有作者所提到的 UnusedByteCodeStripper2.exe 工具，推测 unity 可能在后续版本更新中做了优化。

测试 Attribute 的优化

新建空的项目工程，创建 test.cs , 对其中的 test 字段使用属性元数据。 选择 IL2Cpp 打包方案打包 apk 包，使用 IL2Cppdumper ，反编译查看包体中的 libil2cpp.so ， 对比查看使用了属性以及未使用属性的打包结果。

未使用属性的 attribute 在反编译结果中未找到对应的声明

Managed bytecode stripping with IL2CPP

查找文档发现 unity2017 已经新增了对 IL 代码的裁剪选项，此选项开启后会使用 UnityLinker(is a version of the Mono IL Linker) 对引擎中未引用的代码进行剔除。
剔除工作是基于代码的静态分析，需要注意以下情况，并处理。

• 如果代码中使用了反射来引用，可能会出现运行时引用类型被剔除的报错。
• 项目打包中会有 prefab 资源的提前构建 ab 包，此构建过程在 UnityLinker 调用之前执行，一些类型的引用只存在与 Prefab 中，也会出现类型丢失问题。需要手动排查并引用进 mono 防止类型被剔除。

执行

对裁剪后的包进行冒烟测试，查找并修复类型丢失的问题。

运行时，unity 会抛出类型丢失的错误，并附带一个应用 ID， 通过 ClassIDRefrence 查找，获知对应的类型。

反射引用

测试下来并未出现有相关类型报错的问题，说明代码中没有通过这种方法对类型进行引用。

资源 ab 包

出现一些 Prefab 引用类型丢失的情况，新增 link.xml 放置在 Assets 下，指导 UnityLinker 的剔除保留。

1
2
3
4
5
6
7
8
9
10
11
12
13

<?xml version="1.0" encoding="utf-8" ?>
<linker>
    <assembly fullname="System">
        <type fullname="System.ComponentModel.TypeConverter" preserve="all" />
    </assembly>
    <assembly fullname="mscorlib">
        <namespace fullname="System.Security.Cryptography" preserve="all"/>
    </assembly>
    <assembly fullname="UnityEngine">
        <type fullname="UnityEngine.Flare" preserve="all"/>
        <type fullname="UnityEngine.Avatar" preserve="all"/>
    </assembly>
</linker>

结果

最终包体缩小 34MB

Managed bytecode stripping with IL2CPP

目标

项目中为了减少打包后的包体大小，针对 IL2CPP 的打包方案做包体缩小的优化

问题

IL2CPP 虽然在性能上比 mono 有优势，但是当代码量增多时，包体会增大

研究

2015 年的一篇帖子有提到 IL2CPP 在打包时会将未使用的属性打包进 IL 中，作者测评下来发现修改裁剪工具，剔除不需要的属性能减少 6% 的 IL2Cpp 大小。
原帖地址
在 unity2017 版本中，并没有作者所提到的 UnusedByteCodeStripper2.exe 工具，推测 unity 可能在后续版本更新中做了优化。

测试 Attribute 的优化

新建空的项目工程，创建 test.cs , 对其中的 test 字段使用属性元数据。 选择 IL2Cpp 打包方案打包 apk 包，使用 IL2Cppdumper ，反编译查看包体中的 libil2cpp.so ， 对比查看使用了属性以及未使用属性的打包结果。

未使用属性的 attribute 在反编译结果中未找到对应的声明

Managed bytecode stripping with IL2CPP

查找文档发现 unity2017 已经新增了对 IL 代码的裁剪选项，此选项开启后会使用 UnityLinker(is a version of the Mono IL Linker) 对引擎中未引用的代码进行剔除。
剔除工作是基于代码的静态分析，需要注意以下情况，并处理。

• 如果代码中使用了反射来引用，可能会出现运行时引用类型被剔除的报错。
• 项目打包中会有 prefab 资源的提前构建 ab 包，此构建过程在 UnityLinker 调用之前执行，一些类型的引用只存在与 Prefab 中，也会出现类型丢失问题。需要手动排查并引用进 mono 防止类型被剔除。

执行

对裁剪后的包进行冒烟测试，查找并修复类型丢失的问题。

运行时，unity 会抛出类型丢失的错误，并附带一个应用 ID， 通过 ClassIDRefrence 查找，获知对应的类型。

反射引用

测试下来并未出现有相关类型报错的问题，说明代码中没有通过这种方法对类型进行引用。

资源 ab 包

出现一些 Prefab 引用类型丢失的情况，新增 link.xml 放置在 Assets 下，指导 UnityLinker 的剔除保留。

1
2
3
4
5
6
7
8
9
10
11
12
13

<?xml version="1.0" encoding="utf-8" ?>
<linker>
    <assembly fullname="System">
        <type fullname="System.ComponentModel.TypeConverter" preserve="all" />
    </assembly>
    <assembly fullname="mscorlib">
        <namespace fullname="System.Security.Cryptography" preserve="all"/>
    </assembly>
    <assembly fullname="UnityEngine">
        <type fullname="UnityEngine.Flare" preserve="all"/>
        <type fullname="UnityEngine.Avatar" preserve="all"/>
    </assembly>
</linker>

结果

最终包体缩小 34MB

查找文档发现 unity2017 已经新增了对 IL 代码的裁剪选项，此选项开启后会使用 UnityLinker(is a version of the Mono IL Linker) 对引擎中未引用的代码进行剔除。
剔除工作是基于代码的静态分析，需要注意以下情况，并处理。

• 如果代码中使用了反射来引用，可能会出现运行时引用类型被剔除的报错。
• 项目打包中会有 prefab 资源的提前构建 ab 包，此构建过程在 UnityLinker 调用之前执行，一些类型的引用只存在与 Prefab 中，也会出现类型丢失问题。需要手动排查并引用进 mono 防止类型被剔除。

执行

对裁剪后的包进行冒烟测试，查找并修复类型丢失的问题。

运行时，unity 会抛出类型丢失的错误，并附带一个应用 ID， 通过 ClassIDRefrence 查找，获知对应的类型。

反射引用

测试下来并未出现有相关类型报错的问题，说明代码中没有通过这种方法对类型进行引用。

资源 ab 包

出现一些 Prefab 引用类型丢失的情况，新增 link.xml 放置在 Assets 下，指导 UnityLinker 的剔除保留。

1
2
3
4
5
6
7
8
9
10
11
12
13

<?xml version="1.0" encoding="utf-8" ?>
<linker>
    <assembly fullname="System">
        <type fullname="System.ComponentModel.TypeConverter" preserve="all" />
    </assembly>
    <assembly fullname="mscorlib">
        <namespace fullname="System.Security.Cryptography" preserve="all"/>
    </assembly>
    <assembly fullname="UnityEngine">
        <type fullname="UnityEngine.Flare" preserve="all"/>
        <type fullname="UnityEngine.Avatar" preserve="all"/>
    </assembly>
</linker>

结果

最终包体缩小 34MB

目标

项目中为了减少打包后的包体大小，针对 IL2CPP 的打包方案做包体缩小的优化

问题

IL2CPP 虽然在性能上比 mono 有优势，但是当代码量增多时，包体会增大

研究

2015 年的一篇帖子有提到 IL2CPP 在打包时会将未使用的属性打包进 IL 中，作者测评下来发现修改裁剪工具，剔除不需要的属性能减少 6% 的 IL2Cpp 大小。
原帖地址
在 unity2017 版本中，并没有作者所提到的 UnusedByteCodeStripper2.exe 工具，推测 unity 可能在后续版本更新中做了优化。

测试 Attribute 的优化

新建空的项目工程，创建 test.cs , 对其中的 test 字段使用属性元数据。 选择 IL2Cpp 打包方案打包 apk 包，使用 IL2Cppdumper ，反编译查看包体中的 libil2cpp.so ， 对比查看使用了属性以及未使用属性的打包结果。

未使用属性的 attribute 在反编译结果中未找到对应的声明

Managed bytecode stripping with IL2CPP

查找文档发现 unity2017 已经新增了对 IL 代码的裁剪选项，此选项开启后会使用 UnityLinker(is a version of the Mono IL Linker) 对引擎中未引用的代码进行剔除。
剔除工作是基于代码的静态分析，需要注意以下情况，并处理。

• 如果代码中使用了反射来引用，可能会出现运行时引用类型被剔除的报错。
• 项目打包中会有 prefab 资源的提前构建 ab 包，此构建过程在 UnityLinker 调用之前执行，一些类型的引用只存在与 Prefab 中，也会出现类型丢失问题。需要手动排查并引用进 mono 防止类型被剔除。

执行

对裁剪后的包进行冒烟测试，查找并修复类型丢失的问题。

运行时，unity 会抛出类型丢失的错误，并附带一个应用 ID， 通过 ClassIDRefrence 查找，获知对应的类型。

反射引用

测试下来并未出现有相关类型报错的问题，说明代码中没有通过这种方法对类型进行引用。

资源 ab 包

出现一些 Prefab 引用类型丢失的情况，新增 link.xml 放置在 Assets 下，指导 UnityLinker 的剔除保留。

1
2
3
4
5
6
7
8
9
10
11
12
13

<?xml version="1.0" encoding="utf-8" ?>
<linker>
    <assembly fullname="System">
        <type fullname="System.ComponentModel.TypeConverter" preserve="all" />
    </assembly>
    <assembly fullname="mscorlib">
        <namespace fullname="System.Security.Cryptography" preserve="all"/>
    </assembly>
    <assembly fullname="UnityEngine">
        <type fullname="UnityEngine.Flare" preserve="all"/>
        <type fullname="UnityEngine.Avatar" preserve="all"/>
    </assembly>
</linker>

结果

最终包体缩小 34MB

目标

项目中为了减少打包后的包体大小，针对 IL2CPP 的打包方案做包体缩小的优化

问题

IL2CPP 虽然在性能上比 mono 有优势，但是当代码量增多时，包体会增大

研究

2015 年的一篇帖子有提到 IL2CPP 在打包时会将未使用的属性打包进 IL 中，作者测评下来发现修改裁剪工具，剔除不需要的属性能减少 6% 的 IL2Cpp 大小。
原帖地址
在 unity2017 版本中，并没有作者所提到的 UnusedByteCodeStripper2.exe 工具，推测 unity 可能在后续版本更新中做了优化。

测试 Attribute 的优化

新建空的项目工程，创建 test.cs , 对其中的 test 字段使用属性元数据。 选择 IL2Cpp 打包方案打包 apk 包，使用 IL2Cppdumper ，反编译查看包体中的 libil2cpp.so ， 对比查看使用了属性以及未使用属性的打包结果。

未使用属性的 attribute 在反编译结果中未找到对应的声明

Managed bytecode stripping with IL2CPP

查找文档发现 unity2017 已经新增了对 IL 代码的裁剪选项，此选项开启后会使用 UnityLinker(is a version of the Mono IL Linker) 对引擎中未引用的代码进行剔除。
剔除工作是基于代码的静态分析，需要注意以下情况，并处理。

• 如果代码中使用了反射来引用，可能会出现运行时引用类型被剔除的报错。
• 项目打包中会有 prefab 资源的提前构建 ab 包，此构建过程在 UnityLinker 调用之前执行，一些类型的引用只存在与 Prefab 中，也会出现类型丢失问题。需要手动排查并引用进 mono 防止类型被剔除。

执行

对裁剪后的包进行冒烟测试，查找并修复类型丢失的问题。

运行时，unity 会抛出类型丢失的错误，并附带一个应用 ID， 通过 ClassIDRefrence 查找，获知对应的类型。

反射引用

测试下来并未出现有相关类型报错的问题，说明代码中没有通过这种方法对类型进行引用。

资源 ab 包

出现一些 Prefab 引用类型丢失的情况，新增 link.xml 放置在 Assets 下，指导 UnityLinker 的剔除保留。

1
2
3
4
5
6
7
8
9
10
11
12
13

<?xml version="1.0" encoding="utf-8" ?>
<linker>
    <assembly fullname="System">
        <type fullname="System.ComponentModel.TypeConverter" preserve="all" />
    </assembly>
    <assembly fullname="mscorlib">
        <namespace fullname="System.Security.Cryptography" preserve="all"/>
    </assembly>
    <assembly fullname="UnityEngine">
        <type fullname="UnityEngine.Flare" preserve="all"/>
        <type fullname="UnityEngine.Avatar" preserve="all"/>
    </assembly>
</linker>

结果

最终包体缩小 34MB

概念

序列化是为了将对象存储（或传输）到内存、数据库或文件中，把对象状态转化为一组字节的过程

概念

序列化是为了将对象存储（或传输）到内存、数据库或文件中，把对象状态转化为一组字节的过程

Unity 如何序列化

Unity 中 UnityEngine.Object 类提供序列化能力，任何继承自它的类（MonoBehaviour,ScriptableObject）， 都可被序列化。 其中大部分使用都是隐形的，开发中不需要在意。

MonoBehavior 编写

可被序列化的字段必须符合以下几点：

• 设为public，或者添加[SerializeField]属性
• 不要设为static
• 不要设为const
• 不要设为readonly
• 字段类型必须是可以序列化的类型

哪些类型可以序列化？

• 来自UntiyEngine.Object的对象引用
• 有 [Serializable] 属性的自定义非抽象类
• 基础数据类型（int，float，double，bool，string等等）
• 可序列化的数组Array字段类型
• 可序列化的泛型列表List字段类型
  结构体

一个很常见的不可被序列化的数据结构：Dictionaries，即使把它们声明为公有并且有 [SerializeField] 属性。在开发游戏时要记住这点。

自定义序列化类型

添加 [System.Serializable] 修饰符

1
2
3
4
5

[System.Serializable]
public class TestData
{
    public BehaviorNode obj;
}

会出现的问题

• 任然依赖于 MonoBehaviour 并且需要 GameObject 才可存在
• 无法支持多态，对一个基类数组添加三个同样的子类对象，序列化后是三个基类对象。
• 耦合引用, 对一个泛型列表添加同一个对象三次，序列化后是三个不同的对象。
• 递归声明
  自定义类型的序列化不支持空引用，在递归引用时，会陷入循环创建的的死循环。 unity 为解决这个问题，限制了最大层深度为 7 层。

解决方法 ScriptableObjects

• 可存储为 xx.asset 资源，不再依托于 GameObject
• ScriptableObjects 继承自 Unity.Object， 在序列化时创建的是对象的引用。

Unity Edtior 对序列化数据的使用

Editor 通过修改序列化数据修改以及显示目标对象

操作 API

EditorWIndow

创建一个窗口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

public class EditStartWindow: EditorWindow
{
    Editor editor;

    [MenuItem("Behavior/Edit")]
    public static void ShowWindow()
    {
        EditStartWindow window = EditorWindow.CreateInstance<EditStartWindow>();
        window.Show();
    }
     private void OnGUI()
    {
        if (GUILayout.Button("Open"))
        {
        }
    }
}

Inspector

定制 Class 在 Inspector 中的显示

1
2
3
4
5
6
7
8
9
10
11
12
13
14

[CustomEditor(typeof(BehaviorRunTime))]
public class BehaviorRunTimeEditor: Editor
{
    public override void OnInspectorGUI()
    {
        base.OnInspectorGUI();

        if (GUILayout.Button("Run"))
        {
            BehaviorRunTime runTime = target as BehaviorRunTime;
            runTime.Invoke("Run", 0);
        }
    }
}

CustomPropertyDrawer

自定义字段的显示方案

• PropertyDrawer
  对自定义属性的字段调用此方法渲染

• DecoratorDrawer
  以装饰模式进行渲染，区别是

  • 不会改变检查器的原始行为，而是扩展它
  • 一个属性上能加不止一个DecoratorDrawer
  • 数组或List上加DecoratorDrawer只会对第一个起作用。
    

问题的解决

不可序列化的类型

• 高维数组低维化，底层使用一维数组来替代
• 字典把 Key 和 Value 各种存储为 List , 运行时用字典，序列化时用数组

自定义序列化接口

ISerializationCallbackReceiver
Unity 提供的一个接口，通过实现 OnBeforeSerialize 和 OnAfterDeserialize 使的原本不能被序列化成功的类可以被加工成合格的类型。

.Net 序列化机制

通过实现 ISerializable 自定义序列化和反序列化过程

另外还有其它的解决方案：
Json Xml yaml 和 二进制

新的版本支持 2019.x

新增 [SerializeReference] 支持对引用类型序列化，支持接口以及抽象类

PS：

• 引用的类必须是可序列化类型
• 引用值无法在 UnityEngine.Object 实例间进行共享

总结

在使用 Unity 的序列化时必须明确了解那些字段能够被序列化，从而减少因为序列化，反序列化后对象数据不一致导致的问题。

Unity 如何序列化

Unity 中 UnityEngine.Object 类提供序列化能力，任何继承自它的类（MonoBehaviour,ScriptableObject）， 都可被序列化。 其中大部分使用都是隐形的，开发中不需要在意。

MonoBehavior 编写

可被序列化的字段必须符合以下几点：

• 设为public，或者添加[SerializeField]属性
• 不要设为static
• 不要设为const
• 不要设为readonly
• 字段类型必须是可以序列化的类型

哪些类型可以序列化？

• 来自UntiyEngine.Object的对象引用
• 有 [Serializable] 属性的自定义非抽象类
• 基础数据类型（int，float，double，bool，string等等）
• 可序列化的数组Array字段类型
• 可序列化的泛型列表List字段类型
  结构体

一个很常见的不可被序列化的数据结构：Dictionaries，即使把它们声明为公有并且有 [SerializeField] 属性。在开发游戏时要记住这点。

自定义序列化类型

添加 [System.Serializable] 修饰符

1
2
3
4
5

[System.Serializable]
public class TestData
{
    public BehaviorNode obj;
}

会出现的问题

• 任然依赖于 MonoBehaviour 并且需要 GameObject 才可存在
• 无法支持多态，对一个基类数组添加三个同样的子类对象，序列化后是三个基类对象。
• 耦合引用, 对一个泛型列表添加同一个对象三次，序列化后是三个不同的对象。
• 递归声明
  自定义类型的序列化不支持空引用，在递归引用时，会陷入循环创建的的死循环。 unity 为解决这个问题，限制了最大层深度为 7 层。

解决方法 ScriptableObjects

• 可存储为 xx.asset 资源，不再依托于 GameObject
• ScriptableObjects 继承自 Unity.Object， 在序列化时创建的是对象的引用。

Unity Edtior 对序列化数据的使用

概念

序列化是为了将对象存储（或传输）到内存、数据库或文件中，把对象状态转化为一组字节的过程

Unity 如何序列化

Unity 中 UnityEngine.Object 类提供序列化能力，任何继承自它的类（MonoBehaviour,ScriptableObject）， 都可被序列化。 其中大部分使用都是隐形的，开发中不需要在意。

MonoBehavior 编写

可被序列化的字段必须符合以下几点：

• 设为public，或者添加[SerializeField]属性
• 不要设为static
• 不要设为const
• 不要设为readonly
• 字段类型必须是可以序列化的类型

哪些类型可以序列化？

• 来自UntiyEngine.Object的对象引用
• 有 [Serializable] 属性的自定义非抽象类
• 基础数据类型（int，float，double，bool，string等等）
• 可序列化的数组Array字段类型
• 可序列化的泛型列表List字段类型
  结构体

一个很常见的不可被序列化的数据结构：Dictionaries，即使把它们声明为公有并且有 [SerializeField] 属性。在开发游戏时要记住这点。

自定义序列化类型

添加 [System.Serializable] 修饰符

1
2
3
4
5

[System.Serializable]
public class TestData
{
    public BehaviorNode obj;
}

会出现的问题

• 任然依赖于 MonoBehaviour 并且需要 GameObject 才可存在
• 无法支持多态，对一个基类数组添加三个同样的子类对象，序列化后是三个基类对象。
• 耦合引用, 对一个泛型列表添加同一个对象三次，序列化后是三个不同的对象。
• 递归声明
  自定义类型的序列化不支持空引用，在递归引用时，会陷入循环创建的的死循环。 unity 为解决这个问题，限制了最大层深度为 7 层。

解决方法 ScriptableObjects

• 可存储为 xx.asset 资源，不再依托于 GameObject
• ScriptableObjects 继承自 Unity.Object， 在序列化时创建的是对象的引用。

Unity Edtior 对序列化数据的使用

Editor 通过修改序列化数据修改以及显示目标对象

操作 API

EditorWIndow

创建一个窗口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

public class EditStartWindow: EditorWindow
{
    Editor editor;

    [MenuItem("Behavior/Edit")]
    public static void ShowWindow()
    {
        EditStartWindow window = EditorWindow.CreateInstance<EditStartWindow>();
        window.Show();
    }
     private void OnGUI()
    {
        if (GUILayout.Button("Open"))
        {
        }
    }
}

Inspector

定制 Class 在 Inspector 中的显示

1
2
3
4
5
6
7
8
9
10
11
12
13
14

[CustomEditor(typeof(BehaviorRunTime))]
public class BehaviorRunTimeEditor: Editor
{
    public override void OnInspectorGUI()
    {
        base.OnInspectorGUI();

        if (GUILayout.Button("Run"))
        {
            BehaviorRunTime runTime = target as BehaviorRunTime;
            runTime.Invoke("Run", 0);
        }
    }
}

CustomPropertyDrawer

自定义字段的显示方案

• PropertyDrawer
  对自定义属性的字段调用此方法渲染

• DecoratorDrawer
  以装饰模式进行渲染，区别是

  • 不会改变检查器的原始行为，而是扩展它
  • 一个属性上能加不止一个DecoratorDrawer
  • 数组或List上加DecoratorDrawer只会对第一个起作用。
    

问题的解决

不可序列化的类型

• 高维数组低维化，底层使用一维数组来替代
• 字典把 Key 和 Value 各种存储为 List , 运行时用字典，序列化时用数组

自定义序列化接口

ISerializationCallbackReceiver
Unity 提供的一个接口，通过实现 OnBeforeSerialize 和 OnAfterDeserialize 使的原本不能被序列化成功的类可以被加工成合格的类型。

.Net 序列化机制

通过实现 ISerializable 自定义序列化和反序列化过程

另外还有其它的解决方案：
Json Xml yaml 和 二进制

新的版本支持 2019.x

新增 [SerializeReference] 支持对引用类型序列化，支持接口以及抽象类

PS：

• 引用的类必须是可序列化类型
• 引用值无法在 UnityEngine.Object 实例间进行共享

总结

在使用 Unity 的序列化时必须明确了解那些字段能够被序列化，从而减少因为序列化，反序列化后对象数据不一致导致的问题。

Editor 通过修改序列化数据修改以及显示目标对象

操作 API

EditorWIndow

创建一个窗口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

public class EditStartWindow: EditorWindow
{
    Editor editor;

    [MenuItem("Behavior/Edit")]
    public static void ShowWindow()
    {
        EditStartWindow window = EditorWindow.CreateInstance<EditStartWindow>();
        window.Show();
    }
     private void OnGUI()
    {
        if (GUILayout.Button("Open"))
        {
        }
    }
}

Inspector

定制 Class 在 Inspector 中的显示

1
2
3
4
5
6
7
8
9
10
11
12
13
14

[CustomEditor(typeof(BehaviorRunTime))]
public class BehaviorRunTimeEditor: Editor
{
    public override void OnInspectorGUI()
    {
        base.OnInspectorGUI();

        if (GUILayout.Button("Run"))
        {
            BehaviorRunTime runTime = target as BehaviorRunTime;
            runTime.Invoke("Run", 0);
        }
    }
}

CustomPropertyDrawer

自定义字段的显示方案

• PropertyDrawer
  对自定义属性的字段调用此方法渲染

• DecoratorDrawer
  以装饰模式进行渲染，区别是

  • 不会改变检查器的原始行为，而是扩展它
  • 一个属性上能加不止一个DecoratorDrawer
  • 数组或List上加DecoratorDrawer只会对第一个起作用。

概念

序列化是为了将对象存储（或传输）到内存、数据库或文件中，把对象状态转化为一组字节的过程

Unity 如何序列化

Unity 中 UnityEngine.Object 类提供序列化能力，任何继承自它的类（MonoBehaviour,ScriptableObject）， 都可被序列化。 其中大部分使用都是隐形的，开发中不需要在意。

MonoBehavior 编写

可被序列化的字段必须符合以下几点：

• 设为public，或者添加[SerializeField]属性
• 不要设为static
• 不要设为const
• 不要设为readonly
• 字段类型必须是可以序列化的类型

哪些类型可以序列化？

• 来自UntiyEngine.Object的对象引用
• 有 [Serializable] 属性的自定义非抽象类
• 基础数据类型（int，float，double，bool，string等等）
• 可序列化的数组Array字段类型
• 可序列化的泛型列表List字段类型
  结构体

一个很常见的不可被序列化的数据结构：Dictionaries，即使把它们声明为公有并且有 [SerializeField] 属性。在开发游戏时要记住这点。

自定义序列化类型

添加 [System.Serializable] 修饰符

1
2
3
4
5

[System.Serializable]
public class TestData
{
    public BehaviorNode obj;
}

会出现的问题

• 任然依赖于 MonoBehaviour 并且需要 GameObject 才可存在
• 无法支持多态，对一个基类数组添加三个同样的子类对象，序列化后是三个基类对象。
• 耦合引用, 对一个泛型列表添加同一个对象三次，序列化后是三个不同的对象。
• 递归声明
  自定义类型的序列化不支持空引用，在递归引用时，会陷入循环创建的的死循环。 unity 为解决这个问题，限制了最大层深度为 7 层。

解决方法 ScriptableObjects

• 可存储为 xx.asset 资源，不再依托于 GameObject
• ScriptableObjects 继承自 Unity.Object， 在序列化时创建的是对象的引用。

Unity Edtior 对序列化数据的使用

Editor 通过修改序列化数据修改以及显示目标对象

操作 API

EditorWIndow

创建一个窗口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

public class EditStartWindow: EditorWindow
{
    Editor editor;

    [MenuItem("Behavior/Edit")]
    public static void ShowWindow()
    {
        EditStartWindow window = EditorWindow.CreateInstance<EditStartWindow>();
        window.Show();
    }
     private void OnGUI()
    {
        if (GUILayout.Button("Open"))
        {
        }
    }
}

Inspector

定制 Class 在 Inspector 中的显示

1
2
3
4
5
6
7
8
9
10
11
12
13
14

[CustomEditor(typeof(BehaviorRunTime))]
public class BehaviorRunTimeEditor: Editor
{
    public override void OnInspectorGUI()
    {
        base.OnInspectorGUI();

        if (GUILayout.Button("Run"))
        {
            BehaviorRunTime runTime = target as BehaviorRunTime;
            runTime.Invoke("Run", 0);
        }
    }
}

CustomPropertyDrawer

自定义字段的显示方案

• PropertyDrawer
  对自定义属性的字段调用此方法渲染

• DecoratorDrawer
  以装饰模式进行渲染，区别是

  • 不会改变检查器的原始行为，而是扩展它
  • 一个属性上能加不止一个DecoratorDrawer
  • 数组或List上加DecoratorDrawer只会对第一个起作用。
    

问题的解决

不可序列化的类型

• 高维数组低维化，底层使用一维数组来替代
• 字典把 Key 和 Value 各种存储为 List , 运行时用字典，序列化时用数组

自定义序列化接口

ISerializationCallbackReceiver
Unity 提供的一个接口，通过实现 OnBeforeSerialize 和 OnAfterDeserialize 使的原本不能被序列化成功的类可以被加工成合格的类型。

.Net 序列化机制

通过实现 ISerializable 自定义序列化和反序列化过程

另外还有其它的解决方案：
Json Xml yaml 和 二进制

新的版本支持 2019.x

新增 [SerializeReference] 支持对引用类型序列化，支持接口以及抽象类

PS：

• 引用的类必须是可序列化类型
• 引用值无法在 UnityEngine.Object 实例间进行共享

总结

在使用 Unity 的序列化时必须明确了解那些字段能够被序列化，从而减少因为序列化，反序列化后对象数据不一致导致的问题。

问题的解决

不可序列化的类型

• 高维数组低维化，底层使用一维数组来替代
• 字典把 Key 和 Value 各种存储为 List , 运行时用字典，序列化时用数组

自定义序列化接口

ISerializationCallbackReceiver
Unity 提供的一个接口，通过实现 OnBeforeSerialize 和 OnAfterDeserialize 使的原本不能被序列化成功的类可以被加工成合格的类型。

.Net 序列化机制

通过实现 ISerializable 自定义序列化和反序列化过程

另外还有其它的解决方案：
Json Xml yaml 和 二进制

新的版本支持 2019.x

新增 [SerializeReference] 支持对引用类型序列化，支持接口以及抽象类

PS：

• 引用的类必须是可序列化类型
• 引用值无法在 UnityEngine.Object 实例间进行共享

总结

在使用 Unity 的序列化时必须明确了解那些字段能够被序列化，从而减少因为序列化，反序列化后对象数据不一致导致的问题。

简介

树的数据结构觉得了它能构建成索引结构，且能高效的减少集合的搜索深度，再配合上有序的插入规则，就能进行高效的搜索。这里介绍一种简单的二叉搜索树（BST），BST 的插入规则为，任意节点的左孩子比自身小，右孩子比自身大。

基本操作

插入

时间复杂度：O(log₂N)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

def _insert(self, parent, node):
    ## 这里不处理相同的数
    if parent.value == node.value:
        return
    ## 比较顺序后放入较小的左子树
    elif parent.value > node.value:
        ## 孩子为空，可以插入
        if parent.left == None:
            parent.left = node
            return
        else:
            self._insert(parent.left, node)
            return
    ## 比较顺序后放入较大的右子树
    elif parent.value < node.value:
        ## 孩子为空，可以插入
        if parent.right == None:
            parent.right = node
            return
        else:
            self._insert(parent.right, node)
            return

移除

时间复杂度：O(log₂N)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

def _remove(self,node, key, parent, isLeft):
    ## 搜索节点
    if node == None:
        return
    ## 搜索较大的右子树
    elif node.value < key:
        return self._remove(node.right, key, node, False)
    ## 搜索较的左子树
    elif node.value > key:
        return self._remove(node.left, key, node, True)
    ## 执行移除
    elif node.value == key:
        rmNode = node
        ## 左右子树任意一个为空，都可以直接把另外一个子树提上一层，替换掉移除的节点
        if node.left == None:
            parent.setChild(isLeft, node.right)
        elif parent.right == None:
            parent.setChild(isLeft, node.left)
        else:
        ## 左右子树不为空
            last = node
            ## 在较大的右子树中找到最小的节点与移除的节点进行替换，并移除目标节点
            minNode = node.right
            while minNode.left:
                last = minNode
                minNode = minNode.left
            
            parent.setChild(isLeft, minNode)
            last.setChild(True, None)

        return rmNode

搜索

按照比较顺序进行搜索，可以快速确定目标元素所在子树，减少冗余枝干的遍历操作。

时间复杂度：O(log₂N)

1
2
3
4
5
6
7
8
9

def _search(self, parent, value):
    if parent == None:
        return None, False
    elif parent.value == value:
        return parent,True
    elif parent.value < value:
        return self._search(parent.right, value)
    elif parent.value > value:
        return self._search(parent.left, value)

PS:

BST 的所有操作都与树的深度有关，在插入操作时，如果插入的顺序是有序的，那么 BST 就会变成深度为 N 的一叉树，大大降低搜索效率。所以在初始化时，可以进行随机取数，减少有序的概率。

以下是此数据结构的 python 实现
github:[https://github.com/dupouyer/algo/tree/master/BST]

冒泡排序

冒泡排序

每一轮，从数组头部开始，每两个元素比较大小按大小方向进行交换，直到数组末尾。然后不断的重复这个过程。

数量优化：每 n 轮比较，数组末尾 n 个元素都是确定的，不需要再进行比较。
提前中断： 在一轮比较中，如果未发生元素交换，说明这个数组已经排序好了，可以中断排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

function sort(nums) {
    var hasChange
    for(var i = 0 ; i < nums.length ; i ++ ) {
        hasChange = false;
        for(var j = 0 ; j < nums.length - 1 - i ; j ++) {
            if(nums[j] > nums[j + 1]) {
                var tmp = nums[j + 1];
                nums[j + 1] = nums[j];
                nums[j] = tmp;
                hasChange = true;
            }
        }

        if(!hasChange) {
            break;
        }
    }
}

算法的空间

复杂度上是 o(1)，

时间复杂度

• 最佳：正序数组，需要 n-1 次比较，复杂度为 O(n) 。
• 最坏：逆序数组，需要 n * (n - 1) / 2 次比较，复杂度为 O(n²) 。

插入排序

不断的将未排序的元素插入已排序的数组内。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

function sort(nums) {
    var current;
    for(var i = 0 ; i < nums.length ; i ++) {
        current = nums[i]
        for(var j = i - 1 ; j >= 0 ; j --) {
            if(current > nums[j]) {
                nums[j] = current;
                break;
            }
            else {
                nums[j + 1] = nums[j]
            }
        }
    }
}

算法的空间

复杂度上是 o(1)，

时间复杂度

• 最佳：正序数组，需要 n-1 次比较，复杂度为 O(n) 。
• 最坏：逆序数组，需要 n * (n - 1) / 2 次比较，复杂度为 O(n²) 。

归并排序

核心思路是把大问题分解成两个或者多个子问题，然后再不断的划分下去直到问题能直接解决, 原始问题的解就是子问题的合并。

把数组不断分解成左右两个子数组，直到只剩单个元素，然后再进行排序合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

function sort(nums, lo , hi){
    // 问题到最小子集了
    if(lo >= hi) {
        return
    }

    var mid = lo + int((hi - lo) / 2);
    // 分成两个子问题
    sort(nums, lo, mid);
    sort(nums, mid, hi);

    // 合并两个子问题
    merge(nums, lo, mid, hi);
}

function merge(nums, lo ,mid, hi) {
    var copy = nums.clone();
    var k = lo, i = lo, j = mid;

    while(k <= hi) {
        if(copy[i] < copy[j]) {
            nums[k] = copy[i];
            k ++;
            i ++;
        }
        elseif(copy[j] < copy[i]) {
            nums[k] = copy[j]
            k ++;
            j ++;
        }
        elseif(i > mid) {
            nums[k] = copy[j]
            k ++ ;
            j ++;
        }
        elseif(j > hi) {
            nums[k] = copy[i]
            k ++;
            i ++;
        }
    }
}

空间复杂度

合并是需要拷贝原数组，所以是 O(n)

时间复杂度

对于规模为 n 的问题来说，每次都是分解成 n / 2 的问题，直到规模为 1 ，类似一个二叉树的结构。二叉树的平均深度是 log(n), 所以需要进行 log(n) 层的划分，每一层都要进行一次合并，合并的元素是所有的元素规模为 n ，也就是 O(n) 的复杂度。 那么真题的复杂度就是 O(nlogn)

快速排序

在分治思想上再进一步优化的就是快速排序，在数组中挑选一个基准值，分解成较大和较小的两个子数组，然后以此继续分解子数组直到问题规模为1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

function sort(nums,int lo, int hi) {
    var p = partiton(nums, lo, hi)
    sort(nums, lo , p - 1)
    sort(nums, p + 1, hi)
}

function partiton(nums, lo, hi) {
    var p = swap(nums,random(lo, hi), hi)
    var i,j
    for(i = lo , j  = lo, j < hi ; j ++) {
        if (nums[j] < nums[hi]) {
            swap(nums, i , j);
            i ++
        }
    }
    swap(nums, i , j)
}

空间复杂度

因为不需要合并操作，只采用交换，所以只要 O(1)

时间复杂度

时间上和归并re排序一样是分成了 logn 层， 每一层都要进行 n - 1 次比较，所以复杂度是 O(nlogn)

拓扑排序

和前面介绍的几种排序不同，拓扑排序应用的场合不再是一个简单的数组，而是研究图论里面顶点和顶点连线之间的性质。拓扑排序就是要将这些顶点按照相连的性质进行排序。

拓扑排序的前提是：

1. 图必须没有环
2. 图必须是有向图

统计每个顶点的前驱（入度）, 选择入度为 0 的顶点输出。删除此顶点以及以此顶点为起点的有向边。更新顶点前驱，再次选择入度为 0 的顶点输出、剪边。 持续下去直到最后一个顶点。

算法实现上，核心点是对图的搜索。图的搜索算法分广度搜索和深度搜索。

算法的稳定性

• 冒泡排序
  每次排序都只是相邻元素交换位置，即使元素相等，但是在交换过程中先后顺序并不会发生变化。算法是稳定的
• 插入排序
  插入排序每次都是插入一个有序数组，也不会改变元素的先后关系，算法是稳定的
• 归并排序
  规模为 1 的子问题中，元素的稳定性不会收到破坏。在两个有序数组合并时,我们可以设置两个元素相等时，永远是前一个子数组的数子在前面，这样就保证了排序的稳定。
• 快速排序
  在一次划分大小数组结束时，会对 i 和 j 两个元素进行交换。这个交换过程会破坏稳定性。

每一轮，从数组头部开始，每两个元素比较大小按大小方向进行交换，直到数组末尾。然后不断的重复这个过程。

数量优化：每 n 轮比较，数组末尾 n 个元素都是确定的，不需要再进行比较。
提前中断： 在一轮比较中，如果未发生元素交换，说明这个数组已经排序好了，可以中断排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

function sort(nums) {
    var hasChange
    for(var i = 0 ; i < nums.length ; i ++ ) {
        hasChange = false;
        for(var j = 0 ; j < nums.length - 1 - i ; j ++) {
            if(nums[j] > nums[j + 1]) {
                var tmp = nums[j + 1];
                nums[j + 1] = nums[j];
                nums[j] = tmp;
                hasChange = true;
            }
        }

        if(!hasChange) {
            break;
        }
    }
}

算法的空间

复杂度上是 o(1)，

时间复杂度

• 最佳：正序数组，需要 n-1 次比较，复杂度为 O(n) 。
• 最坏：逆序数组，需要 n * (n - 1) / 2 次比较，复杂度为 O(n²) 。

插入排序

冒泡排序

每一轮，从数组头部开始，每两个元素比较大小按大小方向进行交换，直到数组末尾。然后不断的重复这个过程。

数量优化：每 n 轮比较，数组末尾 n 个元素都是确定的，不需要再进行比较。
提前中断： 在一轮比较中，如果未发生元素交换，说明这个数组已经排序好了，可以中断排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

function sort(nums) {
    var hasChange
    for(var i = 0 ; i < nums.length ; i ++ ) {
        hasChange = false;
        for(var j = 0 ; j < nums.length - 1 - i ; j ++) {
            if(nums[j] > nums[j + 1]) {
                var tmp = nums[j + 1];
                nums[j + 1] = nums[j];
                nums[j] = tmp;
                hasChange = true;
            }
        }

        if(!hasChange) {
            break;
        }
    }
}

算法的空间

复杂度上是 o(1)，

时间复杂度

• 最佳：正序数组，需要 n-1 次比较，复杂度为 O(n) 。
• 最坏：逆序数组，需要 n * (n - 1) / 2 次比较，复杂度为 O(n²) 。

插入排序

不断的将未排序的元素插入已排序的数组内。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

function sort(nums) {
    var current;
    for(var i = 0 ; i < nums.length ; i ++) {
        current = nums[i]
        for(var j = i - 1 ; j >= 0 ; j --) {
            if(current > nums[j]) {
                nums[j] = current;
                break;
            }
            else {
                nums[j + 1] = nums[j]
            }
        }
    }
}

算法的空间

复杂度上是 o(1)，

时间复杂度

• 最佳：正序数组，需要 n-1 次比较，复杂度为 O(n) 。
• 最坏：逆序数组，需要 n * (n - 1) / 2 次比较，复杂度为 O(n²) 。

归并排序

核心思路是把大问题分解成两个或者多个子问题，然后再不断的划分下去直到问题能直接解决, 原始问题的解就是子问题的合并。

把数组不断分解成左右两个子数组，直到只剩单个元素，然后再进行排序合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

function sort(nums, lo , hi){
    // 问题到最小子集了
    if(lo >= hi) {
        return
    }

    var mid = lo + int((hi - lo) / 2);
    // 分成两个子问题
    sort(nums, lo, mid);
    sort(nums, mid, hi);

    // 合并两个子问题
    merge(nums, lo, mid, hi);
}

function merge(nums, lo ,mid, hi) {
    var copy = nums.clone();
    var k = lo, i = lo, j = mid;

    while(k <= hi) {
        if(copy[i] < copy[j]) {
            nums[k] = copy[i];
            k ++;
            i ++;
        }
        elseif(copy[j] < copy[i]) {
            nums[k] = copy[j]
            k ++;
            j ++;
        }
        elseif(i > mid) {
            nums[k] = copy[j]
            k ++ ;
            j ++;
        }
        elseif(j > hi) {
            nums[k] = copy[i]
            k ++;
            i ++;
        }
    }
}

空间复杂度

合并是需要拷贝原数组，所以是 O(n)

时间复杂度

对于规模为 n 的问题来说，每次都是分解成 n / 2 的问题，直到规模为 1 ，类似一个二叉树的结构。二叉树的平均深度是 log(n), 所以需要进行 log(n) 层的划分，每一层都要进行一次合并，合并的元素是所有的元素规模为 n ，也就是 O(n) 的复杂度。 那么真题的复杂度就是 O(nlogn)

快速排序

在分治思想上再进一步优化的就是快速排序，在数组中挑选一个基准值，分解成较大和较小的两个子数组，然后以此继续分解子数组直到问题规模为1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

function sort(nums,int lo, int hi) {
    var p = partiton(nums, lo, hi)
    sort(nums, lo , p - 1)
    sort(nums, p + 1, hi)
}

function partiton(nums, lo, hi) {
    var p = swap(nums,random(lo, hi), hi)
    var i,j
    for(i = lo , j  = lo, j < hi ; j ++) {
        if (nums[j] < nums[hi]) {
            swap(nums, i , j);
            i ++
        }
    }
    swap(nums, i , j)
}

空间复杂度

因为不需要合并操作，只采用交换，所以只要 O(1)

时间复杂度

时间上和归并re排序一样是分成了 logn 层， 每一层都要进行 n - 1 次比较，所以复杂度是 O(nlogn)

拓扑排序

和前面介绍的几种排序不同，拓扑排序应用的场合不再是一个简单的数组，而是研究图论里面顶点和顶点连线之间的性质。拓扑排序就是要将这些顶点按照相连的性质进行排序。

拓扑排序的前提是：

1. 图必须没有环
2. 图必须是有向图

统计每个顶点的前驱（入度）, 选择入度为 0 的顶点输出。删除此顶点以及以此顶点为起点的有向边。更新顶点前驱，再次选择入度为 0 的顶点输出、剪边。 持续下去直到最后一个顶点。

算法实现上，核心点是对图的搜索。图的搜索算法分广度搜索和深度搜索。

算法的稳定性

• 冒泡排序
  每次排序都只是相邻元素交换位置，即使元素相等，但是在交换过程中先后顺序并不会发生变化。算法是稳定的
• 插入排序
  插入排序每次都是插入一个有序数组，也不会改变元素的先后关系，算法是稳定的
• 归并排序
  规模为 1 的子问题中，元素的稳定性不会收到破坏。在两个有序数组合并时,我们可以设置两个元素相等时，永远是前一个子数组的数子在前面，这样就保证了排序的稳定。
• 快速排序
  在一次划分大小数组结束时，会对 i 和 j 两个元素进行交换。这个交换过程会破坏稳定性。

不断的将未排序的元素插入已排序的数组内。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

function sort(nums) {
    var current;
    for(var i = 0 ; i < nums.length ; i ++) {
        current = nums[i]
        for(var j = i - 1 ; j >= 0 ; j --) {
            if(current > nums[j]) {
                nums[j] = current;
                break;
            }
            else {
                nums[j + 1] = nums[j]
            }
        }
    }
}

算法的空间

复杂度上是 o(1)，

时间复杂度

• 最佳：正序数组，需要 n-1 次比较，复杂度为 O(n) 。
• 最坏：逆序数组，需要 n * (n - 1) / 2 次比较，复杂度为 O(n²) 。

归并排序

冒泡排序

每一轮，从数组头部开始，每两个元素比较大小按大小方向进行交换，直到数组末尾。然后不断的重复这个过程。

数量优化：每 n 轮比较，数组末尾 n 个元素都是确定的，不需要再进行比较。
提前中断： 在一轮比较中，如果未发生元素交换，说明这个数组已经排序好了，可以中断排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

function sort(nums) {
    var hasChange
    for(var i = 0 ; i < nums.length ; i ++ ) {
        hasChange = false;
        for(var j = 0 ; j < nums.length - 1 - i ; j ++) {
            if(nums[j] > nums[j + 1]) {
                var tmp = nums[j + 1];
                nums[j + 1] = nums[j];
                nums[j] = tmp;
                hasChange = true;
            }
        }

        if(!hasChange) {
            break;
        }
    }
}

算法的空间

复杂度上是 o(1)，

时间复杂度

• 最佳：正序数组，需要 n-1 次比较，复杂度为 O(n) 。
• 最坏：逆序数组，需要 n * (n - 1) / 2 次比较，复杂度为 O(n²) 。

插入排序

不断的将未排序的元素插入已排序的数组内。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

function sort(nums) {
    var current;
    for(var i = 0 ; i < nums.length ; i ++) {
        current = nums[i]
        for(var j = i - 1 ; j >= 0 ; j --) {
            if(current > nums[j]) {
                nums[j] = current;
                break;
            }
            else {
                nums[j + 1] = nums[j]
            }
        }
    }
}

算法的空间

复杂度上是 o(1)，

时间复杂度

• 最佳：正序数组，需要 n-1 次比较，复杂度为 O(n) 。
• 最坏：逆序数组，需要 n * (n - 1) / 2 次比较，复杂度为 O(n²) 。

归并排序

核心思路是把大问题分解成两个或者多个子问题，然后再不断的划分下去直到问题能直接解决, 原始问题的解就是子问题的合并。

把数组不断分解成左右两个子数组，直到只剩单个元素，然后再进行排序合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

function sort(nums, lo , hi){
    // 问题到最小子集了
    if(lo >= hi) {
        return
    }

    var mid = lo + int((hi - lo) / 2);
    // 分成两个子问题
    sort(nums, lo, mid);
    sort(nums, mid, hi);

    // 合并两个子问题
    merge(nums, lo, mid, hi);
}

function merge(nums, lo ,mid, hi) {
    var copy = nums.clone();
    var k = lo, i = lo, j = mid;

    while(k <= hi) {
        if(copy[i] < copy[j]) {
            nums[k] = copy[i];
            k ++;
            i ++;
        }
        elseif(copy[j] < copy[i]) {
            nums[k] = copy[j]
            k ++;
            j ++;
        }
        elseif(i > mid) {
            nums[k] = copy[j]
            k ++ ;
            j ++;
        }
        elseif(j > hi) {
            nums[k] = copy[i]
            k ++;
            i ++;
        }
    }
}

空间复杂度

合并是需要拷贝原数组，所以是 O(n)

时间复杂度

对于规模为 n 的问题来说，每次都是分解成 n / 2 的问题，直到规模为 1 ，类似一个二叉树的结构。二叉树的平均深度是 log(n), 所以需要进行 log(n) 层的划分，每一层都要进行一次合并，合并的元素是所有的元素规模为 n ，也就是 O(n) 的复杂度。 那么真题的复杂度就是 O(nlogn)

快速排序

在分治思想上再进一步优化的就是快速排序，在数组中挑选一个基准值，分解成较大和较小的两个子数组，然后以此继续分解子数组直到问题规模为1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

function sort(nums,int lo, int hi) {
    var p = partiton(nums, lo, hi)
    sort(nums, lo , p - 1)
    sort(nums, p + 1, hi)
}

function partiton(nums, lo, hi) {
    var p = swap(nums,random(lo, hi), hi)
    var i,j
    for(i = lo , j  = lo, j < hi ; j ++) {
        if (nums[j] < nums[hi]) {
            swap(nums, i , j);
            i ++
        }
    }
    swap(nums, i , j)
}

空间复杂度

因为不需要合并操作，只采用交换，所以只要 O(1)

时间复杂度

时间上和归并re排序一样是分成了 logn 层， 每一层都要进行 n - 1 次比较，所以复杂度是 O(nlogn)

拓扑排序

和前面介绍的几种排序不同，拓扑排序应用的场合不再是一个简单的数组，而是研究图论里面顶点和顶点连线之间的性质。拓扑排序就是要将这些顶点按照相连的性质进行排序。

拓扑排序的前提是：

1. 图必须没有环
2. 图必须是有向图

统计每个顶点的前驱（入度）, 选择入度为 0 的顶点输出。删除此顶点以及以此顶点为起点的有向边。更新顶点前驱，再次选择入度为 0 的顶点输出、剪边。 持续下去直到最后一个顶点。

算法实现上，核心点是对图的搜索。图的搜索算法分广度搜索和深度搜索。

算法的稳定性

• 冒泡排序
  每次排序都只是相邻元素交换位置，即使元素相等，但是在交换过程中先后顺序并不会发生变化。算法是稳定的
• 插入排序
  插入排序每次都是插入一个有序数组，也不会改变元素的先后关系，算法是稳定的
• 归并排序
  规模为 1 的子问题中，元素的稳定性不会收到破坏。在两个有序数组合并时,我们可以设置两个元素相等时，永远是前一个子数组的数子在前面，这样就保证了排序的稳定。
• 快速排序
  在一次划分大小数组结束时，会对 i 和 j 两个元素进行交换。这个交换过程会破坏稳定性。

核心思路是把大问题分解成两个或者多个子问题，然后再不断的划分下去直到问题能直接解决, 原始问题的解就是子问题的合并。

把数组不断分解成左右两个子数组，直到只剩单个元素，然后再进行排序合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

function sort(nums, lo , hi){
    // 问题到最小子集了
    if(lo >= hi) {
        return
    }

    var mid = lo + int((hi - lo) / 2);
    // 分成两个子问题
    sort(nums, lo, mid);
    sort(nums, mid, hi);

    // 合并两个子问题
    merge(nums, lo, mid, hi);
}

function merge(nums, lo ,mid, hi) {
    var copy = nums.clone();
    var k = lo, i = lo, j = mid;

    while(k <= hi) {
        if(copy[i] < copy[j]) {
            nums[k] = copy[i];
            k ++;
            i ++;
        }
        elseif(copy[j] < copy[i]) {
            nums[k] = copy[j]
            k ++;
            j ++;
        }
        elseif(i > mid) {
            nums[k] = copy[j]
            k ++ ;
            j ++;
        }
        elseif(j > hi) {
            nums[k] = copy[i]
            k ++;
            i ++;
        }
    }
}

空间复杂度

合并是需要拷贝原数组，所以是 O(n)

时间复杂度

对于规模为 n 的问题来说，每次都是分解成 n / 2 的问题，直到规模为 1 ，类似一个二叉树的结构。二叉树的平均深度是 log(n), 所以需要进行 log(n) 层的划分，每一层都要进行一次合并，合并的元素是所有的元素规模为 n ，也就是 O(n) 的复杂度。 那么真题的复杂度就是 O(nlogn)

快速排序

在分治思想上再进一步优化的就是快速排序，在数组中挑选一个基准值，分解成较大和较小的两个子数组，然后以此继续分解子数组直到问题规模为1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

function sort(nums,int lo, int hi) {
    var p = partiton(nums, lo, hi)
    sort(nums, lo , p - 1)
    sort(nums, p + 1, hi)
}

function partiton(nums, lo, hi) {
    var p = swap(nums,random(lo, hi), hi)
    var i,j
    for(i = lo , j  = lo, j < hi ; j ++) {
        if (nums[j] < nums[hi]) {
            swap(nums, i , j);
            i ++
        }
    }
    swap(nums, i , j)
}

空间复杂度

因为不需要合并操作，只采用交换，所以只要 O(1)

时间复杂度

时间上和归并re排序一样是分成了 logn 层， 每一层都要进行 n - 1 次比较，所以复杂度是 O(nlogn)

拓扑排序

冒泡排序

每一轮，从数组头部开始，每两个元素比较大小按大小方向进行交换，直到数组末尾。然后不断的重复这个过程。

数量优化：每 n 轮比较，数组末尾 n 个元素都是确定的，不需要再进行比较。
提前中断： 在一轮比较中，如果未发生元素交换，说明这个数组已经排序好了，可以中断排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

function sort(nums) {
    var hasChange
    for(var i = 0 ; i < nums.length ; i ++ ) {
        hasChange = false;
        for(var j = 0 ; j < nums.length - 1 - i ; j ++) {
            if(nums[j] > nums[j + 1]) {
                var tmp = nums[j + 1];
                nums[j + 1] = nums[j];
                nums[j] = tmp;
                hasChange = true;
            }
        }

        if(!hasChange) {
            break;
        }
    }
}

算法的空间

复杂度上是 o(1)，

时间复杂度

• 最佳：正序数组，需要 n-1 次比较，复杂度为 O(n) 。
• 最坏：逆序数组，需要 n * (n - 1) / 2 次比较，复杂度为 O(n²) 。

插入排序

不断的将未排序的元素插入已排序的数组内。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

function sort(nums) {
    var current;
    for(var i = 0 ; i < nums.length ; i ++) {
        current = nums[i]
        for(var j = i - 1 ; j >= 0 ; j --) {
            if(current > nums[j]) {
                nums[j] = current;
                break;
            }
            else {
                nums[j + 1] = nums[j]
            }
        }
    }
}

算法的空间

复杂度上是 o(1)，

时间复杂度

• 最佳：正序数组，需要 n-1 次比较，复杂度为 O(n) 。
• 最坏：逆序数组，需要 n * (n - 1) / 2 次比较，复杂度为 O(n²) 。

归并排序

核心思路是把大问题分解成两个或者多个子问题，然后再不断的划分下去直到问题能直接解决, 原始问题的解就是子问题的合并。

把数组不断分解成左右两个子数组，直到只剩单个元素，然后再进行排序合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

function sort(nums, lo , hi){
    // 问题到最小子集了
    if(lo >= hi) {
        return
    }

    var mid = lo + int((hi - lo) / 2);
    // 分成两个子问题
    sort(nums, lo, mid);
    sort(nums, mid, hi);

    // 合并两个子问题
    merge(nums, lo, mid, hi);
}

function merge(nums, lo ,mid, hi) {
    var copy = nums.clone();
    var k = lo, i = lo, j = mid;

    while(k <= hi) {
        if(copy[i] < copy[j]) {
            nums[k] = copy[i];
            k ++;
            i ++;
        }
        elseif(copy[j] < copy[i]) {
            nums[k] = copy[j]
            k ++;
            j ++;
        }
        elseif(i > mid) {
            nums[k] = copy[j]
            k ++ ;
            j ++;
        }
        elseif(j > hi) {
            nums[k] = copy[i]
            k ++;
            i ++;
        }
    }
}

空间复杂度

合并是需要拷贝原数组，所以是 O(n)

时间复杂度

对于规模为 n 的问题来说，每次都是分解成 n / 2 的问题，直到规模为 1 ，类似一个二叉树的结构。二叉树的平均深度是 log(n), 所以需要进行 log(n) 层的划分，每一层都要进行一次合并，合并的元素是所有的元素规模为 n ，也就是 O(n) 的复杂度。 那么真题的复杂度就是 O(nlogn)

快速排序

在分治思想上再进一步优化的就是快速排序，在数组中挑选一个基准值，分解成较大和较小的两个子数组，然后以此继续分解子数组直到问题规模为1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

function sort(nums,int lo, int hi) {
    var p = partiton(nums, lo, hi)
    sort(nums, lo , p - 1)
    sort(nums, p + 1, hi)
}

function partiton(nums, lo, hi) {
    var p = swap(nums,random(lo, hi), hi)
    var i,j
    for(i = lo , j  = lo, j < hi ; j ++) {
        if (nums[j] < nums[hi]) {
            swap(nums, i , j);
            i ++
        }
    }
    swap(nums, i , j)
}

空间复杂度

因为不需要合并操作，只采用交换，所以只要 O(1)

时间复杂度

时间上和归并re排序一样是分成了 logn 层， 每一层都要进行 n - 1 次比较，所以复杂度是 O(nlogn)

拓扑排序

和前面介绍的几种排序不同，拓扑排序应用的场合不再是一个简单的数组，而是研究图论里面顶点和顶点连线之间的性质。拓扑排序就是要将这些顶点按照相连的性质进行排序。

拓扑排序的前提是：

1. 图必须没有环
2. 图必须是有向图

统计每个顶点的前驱（入度）, 选择入度为 0 的顶点输出。删除此顶点以及以此顶点为起点的有向边。更新顶点前驱，再次选择入度为 0 的顶点输出、剪边。 持续下去直到最后一个顶点。

算法实现上，核心点是对图的搜索。图的搜索算法分广度搜索和深度搜索。

算法的稳定性

• 冒泡排序
  每次排序都只是相邻元素交换位置，即使元素相等，但是在交换过程中先后顺序并不会发生变化。算法是稳定的
• 插入排序
  插入排序每次都是插入一个有序数组，也不会改变元素的先后关系，算法是稳定的
• 归并排序
  规模为 1 的子问题中，元素的稳定性不会收到破坏。在两个有序数组合并时,我们可以设置两个元素相等时，永远是前一个子数组的数子在前面，这样就保证了排序的稳定。
• 快速排序
  在一次划分大小数组结束时，会对 i 和 j 两个元素进行交换。这个交换过程会破坏稳定性。

和前面介绍的几种排序不同，拓扑排序应用的场合不再是一个简单的数组，而是研究图论里面顶点和顶点连线之间的性质。拓扑排序就是要将这些顶点按照相连的性质进行排序。

拓扑排序的前提是：

1. 图必须没有环
2. 图必须是有向图

统计每个顶点的前驱（入度）, 选择入度为 0 的顶点输出。删除此顶点以及以此顶点为起点的有向边。更新顶点前驱，再次选择入度为 0 的顶点输出、剪边。 持续下去直到最后一个顶点。

算法实现上，核心点是对图的搜索。图的搜索算法分广度搜索和深度搜索。

算法的稳定性

• 冒泡排序
  每次排序都只是相邻元素交换位置，即使元素相等，但是在交换过程中先后顺序并不会发生变化。算法是稳定的
• 插入排序
  插入排序每次都是插入一个有序数组，也不会改变元素的先后关系，算法是稳定的
• 归并排序
  规模为 1 的子问题中，元素的稳定性不会收到破坏。在两个有序数组合并时,我们可以设置两个元素相等时，永远是前一个子数组的数子在前面，这样就保证了排序的稳定。
• 快速排序
  在一次划分大小数组结束时，会对 i 和 j 两个元素进行交换。这个交换过程会破坏稳定性。

基本的数据结构类型

数组

最常用的数据结构

在内存中申请一块固定长度连续空间，可通过下标来访问

1

array = malloc(n);

因为内存需要提前申请，所以在使用上如果遇到可变长度的存储需求时，需要频繁申请新的内存块，会有严重的内存开销问题，所以引入了链表

链表

以节点为存储单元，一个节点包含值与下一个节点的地址

1
2
3

linkNode = malloc(2);
linkNode[1] = value;
linkeNode[2] = &nextNode;

可根据存储需求临时开辟存储空间。但是在访问单个节点上效率又没有数组来的快捷，需要从头节点逐个遍历至 i。
现代编程语言大多实现了 List 类型的数据结构综合两者的优缺点，实现了可变长度且可通过下标访问成员。

List

通过内部算法，动态开辟符合长度的内存空间来满足长度需求，不同编程语言的实现方法也会不一样。
一下简述一下个人对于 List 一种实现方案

设置一个合适长度的子数组 (subArray) 长度 k , 根据 List 的长度动态创建以及销毁子数组。
设置一个链表 (nodes) 存储子数组的头节点。
内置长度计数器 count
访问 List[i] = nodes[i % k][int(i / k)]

队列

先进先出，特点是优先处理最早加入的节点

广度搜索中应用此结构辅助记录每次需要搜索的节点。

栈

先进后出，特点是优先处理最近加入的节点

深度搜索中应用此结构辅助记录每次需要搜索的节点。

队列和栈是两个老生常谈的结构，实现方法有多种。在这里就不详述了,需要的可以自行查找。

hash表

给定一个 key 值，通过 hask 函数 adress = hash(key), 获得 key 对应的固定地址。如果有多个key 返回同样的hash值,通过冲突解决函数来获得偏移地址。 hash 表虽然在实现的描述上性能优越，可变长度，快速访问。但是在编程语言中的实现还是需要落在实处，需要基础的数组，链表来实现。

脚本语言中的 Dictionary 类实现

这里举例一个字典的实现。
两个链表，一个 存储 hask 值 一个存储 value 的引用，从图中可以看出，虽然字典获得快速访问优势，但是付出了更多的空间代价。

基本的数据结构类型

数组

最常用的数据结构

在内存中申请一块固定长度连续空间，可通过下标来访问

1

array = malloc(n);

因为内存需要提前申请，所以在使用上如果遇到可变长度的存储需求时，需要频繁申请新的内存块，会有严重的内存开销问题，所以引入了链表

链表

以节点为存储单元，一个节点包含值与下一个节点的地址

1
2
3

linkNode = malloc(2);
linkNode[1] = value;
linkeNode[2] = &nextNode;

可根据存储需求临时开辟存储空间。但是在访问单个节点上效率又没有数组来的快捷，需要从头节点逐个遍历至 i。
现代编程语言大多实现了 List 类型的数据结构综合两者的优缺点，实现了可变长度且可通过下标访问成员。

List

通过内部算法，动态开辟符合长度的内存空间来满足长度需求，不同编程语言的实现方法也会不一样。
一下简述一下个人对于 List 一种实现方案

设置一个合适长度的子数组 (subArray) 长度 k , 根据 List 的长度动态创建以及销毁子数组。
设置一个链表 (nodes) 存储子数组的头节点。
内置长度计数器 count
访问 List[i] = nodes[i % k][int(i / k)]

队列

先进先出，特点是优先处理最早加入的节点

广度搜索中应用此结构辅助记录每次需要搜索的节点。

栈

先进后出，特点是优先处理最近加入的节点

深度搜索中应用此结构辅助记录每次需要搜索的节点。

队列和栈是两个老生常谈的结构，实现方法有多种。在这里就不详述了,需要的可以自行查找。

hash表

给定一个 key 值，通过 hask 函数 adress = hash(key), 获得 key 对应的固定地址。如果有多个key 返回同样的hash值,通过冲突解决函数来获得偏移地址。 hash 表虽然在实现的描述上性能优越，可变长度，快速访问。但是在编程语言中的实现还是需要落在实处，需要基础的数组，链表来实现。

脚本语言中的 Dictionary 类实现

这里举例一个字典的实现。
两个链表，一个 存储 hask 值 一个存储 value 的引用，从图中可以看出，虽然字典获得快速访问优势，但是付出了更多的空间代价。

以上就是编程语言中常用的基础数据结构。后续高级的数据结构都无法脱离数组和链表这两种基础结构，都是以两者为存储单元，再配以存取逻辑来实现的。

以上就是编程语言中常用的基础数据结构。后续高级的数据结构都无法脱离数组和链表这两种基础结构，都是以两者为存储单元，再配以存取逻辑来实现的。

动画

补间动画

补间动画是以关键帧以及补间函数组成，在运行时生成当前的动画信息。
优点：能利用少量的资源展现丰富的表现, 不会受游戏帧率波动影响。
缺点：运行时计算，计算量与动画数量，动画复杂度正相关。
优化方向：anim instance 使用 gpu 计算,目前只有骨骼动画适用

补间函数

根据当前时间计算出动画状态。
公式：state = f(t)

常用补间

模拟自然中的物理规则。
匀速运动，加速运动，减速运动
p = (P2 - P1) / T * t

物理公式：
s = V0 t + a / 2 t ^ 2

缓动方程

tween(t, b , c , d)
t（time）、b（beforeMove）、c（changeDistance）及d（duration）

X轴 时间
Y轴 量

对 x 轴归一化处理
X = dx = t / d (0 -> 1)
Y = dy (0 -> 1)

构建函数 y = x ^ 2 , y = x ^ 3 …..
y = 1 - cos(0.5pi X)
y = sin(0.5pi X)

s = b + c * dy

IK

反向动力学
M = Mij * Mpos

骨骼动画

骨骼，蒙皮，关键帧，补间
关键帧存储骨骼的状态信息，骨骼状态信息是矩阵，可参与补间运算。计算出当前时间的骨骼状态后，再更具顶点中记录的权重信息来计算出顶点跟随骨骼运动后的坐标。

帧动画

以固定帧率播放贴图内容的动画。
优点：表现力强，不受限于动画信息的存储。
缺点：贴图内容与动画长度正相关。占用大量内存空间, 播放帧率不稳定时，会失真。

优化方向：贴图合批，前期规划。

位图混合

多张位图混合，控制其中某几张图的滚动形成动画
shader 运行时，混合多帧位图。
运行时不需要计算帧内容
贴图资源大

利用混合让图片内容动起来

运行时可以通过shader 加入额外的控制参数，动画内容受运行时控制。

噪点的利用

噪点图的参数，在随机性上更自然。 贴图可进入 GPU 运算，效率更佳。

状态机

补充

播放，帧率

总结

anim = controlPoint + f(t)

业务

编程语言

• C#
  • 装箱，拆箱
• C++
  • 内存管理
• Lua
  • class 实现，原表

内存管理

• 美术资源：
  • 纹理压缩，不同格式的纹理进入内存后的体积不一样，针对应用场景进行更加精细的格式控制。
  • UI 上使用公用元素，复用资源。多使用九宫格，减少图片尺寸
  • 网格缩减, 需要展示更多细节的提高面数，离摄像机比较远的使用少的面数，或者使用贴图实现
  • 动画文件优化, 浮点精度减少，关闭缩放
• 对象：
  • 对象池复用对象
  • 大尺寸对象的销毁策略优化
• 脚本：
  • 销毁闲置脚本（不怎么需要处理）

GC

• C# GC
  • 引用计数
• Lua GC
  • 引用计数
  • GC 步长设定(设定策略）
  • 资料：
    https://blog.codingnow.com/2011/03/lua_gc_1.html
    https://blog.codingnow.com/2011/03/lua_gc_2.html

    热更新

• Lua 热更,通过版本文件修改 url
• IL2CPP,性能比较高

  协程

• yeild return new WaitForSeconds(3)
• 异步编程
  do something
  yeild return request()

  C/C++插件

• JAVA <-> JNI <-> C/C++ 桥接 <-> CLR
• IOS <-> OC <-> CLR

CLR(Common Language Runtime)

• 资料：http://www.cnblogs.com/skynet/archive/2010/05/17/1737028.html
• 在 CLR 监管下的运行程序属于 “托管”(managed)代码
• 直接在裸机上运行的应用或者组件属于”非托管”(unmanaged)代码

Unity API

• gameobject.getComponent
• transform
• resource
• collider
• animator
• animation
• animationclip

网络

• TCP,UDP 可靠性区别
• 弱网环境的处理, 保证数据的一致性
  • 有状态同步，服务器保存玩家的所有状态信息
  • 帧同步, 按帧率推进状态

引擎

• 渲染管线:
  顶点 -> 几何 -> 片段 - > 栅格 -> Ztest,Blend -> 后处理
• 物理碰撞的策略:
  • 精细化的选择不同的碰撞体
  • 合理的分层控制碰撞范围
  • 少用，或者不用连续碰撞检测
• Batch:
  • TextureAtlas
  • 静态 batch，资源 build 阶段, 合并物体。
    优势：不消耗计算资源
    劣势：包体增大（生成资源文件用来描述合并后的物体）
  • 动态 batch 运行时，forward render ,CPU 合并 物体
    优势：灵活
    劣势：消耗计算资源切且，U3D 中对一次 batch 的定点数有限制 900 个，对于有透明物体的情况下，不能很好的执行合批。（透明物体有严格的渲染顺序控制）
  • 运行时合批: 调用 Mesh.CombineMeshes 方法合并物体
• 纹理格式:

架构

• MVC
  老生常谈的一个东西了，在业务逻辑的编写上要注意合理的拆分数据与操作逻辑，View 这一层一般都是由第三方的 UI 框架搭建，结构都很内聚。核心在于实现数据驱动。
• UI
  • FariyGUI
  • UGUI
• 面向对象
  • 多使用组合，避免使用继承。
  • 业务逻辑上继承的越多，维护越困难。
  • 多使用方法操作数据
  • 业务数据结构要足够元,才能更好的应对迭代变化, 变化的部分放入方法中。

适配

• UI 解决方案
  • 锚点缩放
  • 按最小尺寸设计布局
• shader
  • 针对低端机器编写

性能优化

代码(CPU):

• 减少业务层的复杂逻辑，运算量大的使用 C# 执行，避免使用 Lua

渲染(GPU):

• 少用实时光照
• shader 优化性能
• LOD 技术
• 遮挡剔除技术
• 合理的 batch

纹理上要避免使用 2048 ，手机端是 CPU 和 GPU 共用一个总线，带宽有限。

数学基础

• 点乘
  |a|*|b|cos0
• 叉乘
  多项式的矩阵表达
• SQT 矩阵
  特殊 4x4 矩阵用来表达 缩放，旋转，平移
• 四元数
  选择的另外一种描述方式
  优点:
  • 可以表达旋转的增量, 进行平滑的插值
  • 没有万向节锁
  • 选择方向反向，直接取反四元数即可
  • 旋转轴可以是任意向量
• 欧拉旋转
  优点：容易理解
  缺点：有方向节锁，无法实现平滑的插值

参考列表：

https://www.jianshu.com/p/10693fee70a5